Между горизонтальными пластинками заряженного плоского конденсатора
находится пылинка массой 10-9 г и с зарядом 3•10-18 Кл. Какова напряженность
поля в конденсаторе, если вес пылинки уравновешен силой воздействия
электрического поля на заряд пылинки?
Дано:
https://a24.club/order-authors/297510?ref=43041c25564d0dda
где β= v/c, с - скорость распространения света.
(1)
связь углового и линейного ускорений
барабана.
.
Дано:
m=10-9 г = 10-12 кг
q=3•10-18 Кл
|
Е= ?
|
Решение:
Пылинка находится в равновесии под действием двух сил: силы
тяжести mg и
силы Fэл, действующей на пылинку со стороны электрического поля.
Так как сила электрического поля должна быть направлена
наверх (точнее против силы тяжести), то и вектор напряженности поля E также будет направлен наверх, поскольку заряд
пылинки q —
положительный.
Запишем первый
закон Ньютона в проекции на ось y:
Лампа в 200 св находится на расстоянии 2 м от лежащей на столе книги.
Освещенность книги 25 лк. Определить, под каким углом падает свет на книгу и на
какой высоте подвешена лампа над столом.
Дано:
I =
200 св
r =2 м
E = 25 лк
|
α = ?
h - ?
|
Решение:
Точечный источник силой света I создает
на площадке, отстоящей от него на расстоянии r, освещенность
где α — угол падения лучей.
Отсюда
Исходя из геометрических представлений, лампочка
висит на высоте
При какой относительной скорости движения релятивистское сокращение длины
движущегося тела составит 50%? (0,87с).
Дано:
l = 0,5 l0
|
v - ?
|
Решение:
Длина l тела, движущегося со скоростью v относительно
некоторой системы отсчета, связана с длиной l0 тела,
неподвижного в этой системе, соотношением
где β= v/c, с - скорость распространения света.
Зная β, находим v
Маховик
и легкий шкив насажены на горизонтальную ось. К шкиву с помощью нити привязан
груз, который, опускаясь равноускоренно, прошел 2 м за 4 с. Момент инерции
маховика 0,05кг×м2 . Определить
массу груза, если радиус шкива 6 см. Массой шкива пренебречь.
Дано:
|
Решение:
 |
На
груз действуют силы: тяжести mg - вниз; натяжения нити T - вверх.
На
барабан действует сила натяжение нити T, приложенная к ободу барабана. Эта сила создаёт
вращающий момент, т.к. она приложена в точке касания нити и барабана. Плечо
этой силы равно R
– радиусу барабана.
На барабан, кроме того, действует сила давления на ось барабана,
уравновешенная силой реакции барабана.
Составим
уравнение движения тел системы в векторном виде:
груз:
барабан:
Выберем
систему координат. Ось X направим по направлению ускорения груза.
Определим
направление углового ускорения и момента силы. Вращение барабана происходит
против часовой стрелки, значит вектор момента силы направлен перпендикулярно
плоскости чертежа вверх (т.е. к нам). Пусть ось Y для барабана совпадает с направлением вектора
момента силы и ε.
Запишем
проекции сил на оси координат, чтобы решить векторное уравнение:
(1)
Решим полученную систему:
М = Т R – численное значение момента силы, где R – плечо силы Т;
связь углового и линейного ускорений
барабана.
Тогда
Т = m (g – a) из уравнения (2);
М = m(g – a)R.
Подставив это выражение в уравнение (2), найдём
Так как груз
опускается равноускоренно, ускорение равно
.
Тогда
Движения двух материальных точек выражаются
уравнениями: x1
= A1+B1t+C1t2, x2
= A2+B2t+C2t2, где A1 = 20 м, A2 = 2 м, B1 = B2 = 2 м/с, C1 = –4 м/с2, С2 = 0,5 м/с2. Определить скорость второй
точки относительно первой в момент времени t = 2 c.
Решение
Дано:
x1
= A1+B1t+C1t2,
x2 = A2+B2t+C2t2,
A1 = 20 м,
A2 = 2 м,
B1
= B2
= 2 м/с,
C1
= –4 м/с2,
С2 = 0,5 м/с2.
t = 2с
|
Скорость есть производная перемещения
по времени.
Скорость второй точки относительно
первой в момент времени
t
= 2 c
 |
V(t) = ?
|
Мяч массой m = 300 г, брошенный горизонтально
со скоростью v0 = 20 м/с, упал на землю под углом 60о к её
поверхности со скоростью v = 40 м/с. Через какое время приземлился мяч, если за
время полёта на него действовала суммарная средняя сила <F> = 5 Н.
Дано:
m = 300 г = 0,3 кг
v0 = 20 м/с
v = 40 м/с
α = 60о
<F> = 5 Н.
|
Средняя сила, действующая на тело в
течение времени
  изменение импульса.
В нашем случае
 |
t
= ?
|
Вагон, скатившись с сортировочной горки,
соединился с помощью автосцепки с двумя такими же вагонами, стоящими на пути.
Определить долю ω механической энергии, потерянной
при сцепке. Трением колёс пренебречь.
Дано:
m
M=3m
|
Решение. Доля энергии, потерянной
при сцепке, выразится соотношением:
где T1 – кинетическая энергия вагона
до автосцепки, ν
– его скорость до автосцепки; u и T'2 – соответственно
скорость и кинетическая энергия вагонов после автосцепки.
Как видно из выражения, для
определения ω
надо найти u.
Воспользуемся тем, что при ударе упругих тел одновременно выполняются два
закона сохранения: импульса и механической энергии.
По закону сохранения импульса,
учитывая, что два вагона до автосцепки покоились, имеем:
 |
ω
= ?
|
Учитывая условия задачи
Тело массой m = 1,00 кг , двигаясь по
горизонтальной поверхности, сталкивается с горизонтальной пружиной,
жесткость которой k = 0,20
кН/м, а масса пренебрежимо мала. Тело сжимает пружину
на s = 1,0 см , считая от ее недеформированного
положения. Коэффициент трения между телом и поверхностью m = 0,50.
Какова скорость тела в момент соударения ?
Решение
|
|||||
m = |
Изменение
кинетической энергии тела равно
работе
|
||||
k = 0,20 кН/м
|
сил, действующих на него:
|
||||
s =
|
DWк = Wк2 – Wк1 = А.
|
(1)
|
|||
m = 0,50
|
В рассматриваемом случае
|
||||
Wк1 = mv 2 / 2, Wк2 = 0.
|
|||||
v - ?
|
Внешними
силами являются сила
трения скольжения
|
||||
 |
(2)
|
||||
где N -
сила реакции опоры,
и сила упругости
пружины
 |
(3)
|
где r - величина деформации.
Так как N = mg, то
модуль силы трения равен
Fтр = m mg .
Работа силы трения на
пути s равна
Атр = – m mgs .
|
(4)
|
Работа силы упругости
при сжатии пружины
на величину s
 |
(5)
|
Из (1),(4),(5)
следует:
 |
(3)
|
Таким
образом
 . |
(4)
|
Проверка (4) на размерность:
[v ] = (( м/с2)м + (Н/м)м2/кг)0,5 = ( м2/с2 + (кг× м/м× с2)м2/кг)0,5 = м/с.
Вычисления:
v = (2 × 0,50×9,8×10-2 + 0,20×103× 10- 4/ 1,0) 0,5
= 3,4 (м/с) .
Ответ
: скорость тела в момент
соударения v = 3,4 м/с.
Больше задач здесь
Проверка формул (5),(6) на размерность:
Молярная масса смеси
находится по формуле
Больше задач здесь
В
сосуде объемом 30 л находится смесь водорода и гелия при температуре 300 К и давлении 832 кПа. Масса смеси
равна 24 г. Определить массу водорода, массу гелия,
плотность и молярную массу смеси.
Решение
|
||||
V = 3,0×10-
|
Для
каждой компоненты данной смеси применимо уравнение
Менделеева-Клапейрона:
|
|||
Т = 300 К
|
p1 V
= m1 RT/ m1 ;
|
(1)
|
||
p = 8,32 ×105 Па
|
p2 V
= m2 RT/ m2 ,
|
(2)
|
||
m = 2,4×10-2 кг |
где
p1 – парциальное давление
водорода, m1 – масса
|
|||
m1 = 2 ×10-3 кг/моль
|
водорода, m1 – его молярная масса, V – объем сосуда,
|
|||
m2 = 4 ×10-3 кг/моль
|
Т – температура газа, R = 8,31 Дж/(моль×К) – универ-
|
|||
сальная
газовая постоянная, p2 – парциальное
|
||||
m1, m2, r, m - ?
|
давление гелия, m2 – масса гелия,
m2 – его молярная
|
|||
масса.
|
||||
Согласно закону Дальтона давление смеси газов
равно сумме парциальных давлений
компонент данной смеси :
p = p1 + p2 .
|
(3)
|
Из
(1)-(3) следует:
p V = ( m1 / m1 + m2 / m2 ) RT
|
(4)
|
Так
как m = m1 + m2 , то из
(4) следуют выражения для массы водорода
и массы гелия:
m1 =
m1 ( m2 pV/ RT - m ) / (m2 - m1)
|
(5)
|
||
m2 =
m2 ( m - m1 pV/ RT ) / (m2 - m1)
|
(6)
|
[ m] = ( кг/моль)(( кг/моль)Па×м3/(Дж/(моль×К) ×К - m)/(кг/моль) = кг×Н×м×/Дж = кг.
Плотность вещества
определяется формулой :
r = m / V .
|
(7)
|
m = m / (n1 + n2),
|
(8)
|
г де n1 = m1 / m1, n2 = m2 / m2 - число молей
водорода и гелия соответственно.
Из (
4) и (8) следует:
m = m RT / p V.
|
(9)
|
Проверка формулы (9)
на размерность:
[m] = кг (Дж/(моль×К)) ×К / Па×м3 = (кг /моль) Дж / Н×м = кг /моль
Вычисления:
m1 = 2×10-3(4×10-3×8,32×105×3,0×10-2/ 8,31×300-2,4×10-2)/ (4- 2)×10-3
= 1,6×10-2 (кг);
m2 =
4×10-3(2,4×10-2 - 2×10-3×8,3×105 ×2,0×10-2/ 8,31×300)/ (4- 2)×10-3 = 0,8×10-2 (кг);
r = 2,4×10-2 / 3,0×10-2 = 0,80 (кг/м3);
m = 0,240 ×8,31× 300/ 830×103× 0,200 = 3,60×10-3 (кг /моль).
Ответ
: масса водорода m1 = 16 г ; масса
гелия m2 = 8 г ;
плотность
смеси r = 0,80 кг/м3; молярная масса
смеси m = 3,60×10-3 кг /моль.
Больше задач здесь
Объем
углекислого газа, находящегося под давлением
110 кПа, увеличился от 1,00 л до 2,00 л
. Определить количество теплоты, изменение
внутренней энергии и работу расширения
газа , если расширение происходило 1) изотермически; 2) изобарно; 3) адиабатно.
Решение
|
|||||||
p = 1,10×105
Па
|
Согласно
первому началу термодинамики, количество
|
||||||
V1
=1,00 ×10-
|
теплоты Q,
полученное газом, расходуется на
|
||||||
V2 =2,00 ×10-
m = 44 ×10-3 кг/моль |
увеличение
его внутренней энергии
U и на
совершенную им работу А :
|
||||||
i = 6
|
Q = DU +
А.
|
(1)
|
|||||
1) Т =
const
|
Внутренняя
энергия идеального газа
определяется
|
||||||
2) p = const
|
выражением
:
|
||||||
3) Q = 0
|
U
= ( i /2) m RT/ m
|
(2)
|
|||||
DU ; А; Q - ?
|
или
с учетом уравнения Менделеева-Клапейрона:
|
||||||
p V = m RT/ m
|
(3)
|
||||||
U = ( i /2) p V ,
|
(4)
|
||||||
где p, Т , V , m – давление
температура , объем и
масса газа, m. i - молярная масса газа и
число степеней свободы его молекул.
Работа газа при изменении
его объема определяется по формуле :
 |
(5)
|
1) В изотермическом
процессе (Т = const) согласно (2) U = const, DU=0 .
Так
как
p = m RT/ V m , то
 |
(6)
|
Проверка формулы (6)
на размерность:
[А] =
Па × м 3 = Н× м = Дж .
Вычисления:
[А] = 1,10×105 × 1,00 ×10-3 × ln 2 = 76 (Дж).
Согласно (1) в данном случае Q = А.
2) В
изобарном процессе ( p = const ) согласно (4)
D U
= ( i /2) p (
V2
- V1 )
,
|
(7)
|
Проверка формулы (7)
на размерность:
[ D U ] = Па × м 3 = Н× м = Дж .
Вычисления:
D U = ( 6/2) × 1,10×105 × ( 2,00 ×10-3 - 1,00 ×10-3) = 330 (Дж).
Согласно (5) в данном случае
А =
p ( V2 - V1 )
|
(8)
|
Проверка формулы (8)
на размерность:
[ А ] = Па × м 3 = Н× м =
Дж .
Вычисления:
А = 1,10×105 × ( 2,00 ×10-3 - 1,00 ×10-3) = 110 (Дж).
Количество
теплоты, полученное газом в данном процессе
в соответствии с (1), (7), (8)
находится по формуле
Q = (( i /2) + 1
) p ( V2 - V1 )
|
(9)
|
Проверка формулы (9) на размерность аналогична
проверке формул (7) и
(8).
Вычисления:
Q = (3
+1) × 1,10×105 × ( 2,00 ×10-3 - 1,00 ×10-3) = 440 (Дж).
В адиабатном процессе ( Q = 0
) согласно (1)
DU = - А.
|
(10)
|
Вычисление величины
DU в данном случае проводится
с помощью формулы (4):
D U
= ( i /2) ( p2 V2
- p1 V1 )
|
(11)
|
В соответствии с
уравнением Пуассона
p V g = const,
|
(12)
|
где g = ( i + 2 )/ i
p2 = p1 (V1 /V 2)g.
|
(13)
|
Согласно (10),
(11),(12)
D U
= ( i /2) p1V1 ((V1 /V 2)g-1 - 1 )
|
(14)
|
||
А = ( i /2) p1 V1 ( 1 - (V1 /V 2)g-1 )
|
(15)
|
Проверка формул (14),(15) на
размерность аналогична проверке формул (7) и (8).
Вычисления:
g = ( 6 + 2 )/6 = 1,33; D U = 3 × 1,10×105 × 1,00 ×10-3 ( 0,5 0,4 - 1) = - 73,2
(Дж);
А
= 61 Дж.
Ответ : 1) в изотермическом процессе
D U = 0; А = 76 Дж. Q = 76 Дж;
2) в
изобарном процессе D U = 330 Дж ; А = 110
Дж; Q = 440 Дж;
3) в адиабатном
процессе D U = - 73,2 Дж; А =73,2
Дж; Q = 0.
Больше задач здесь
 
Источник тока замкнули на катушку, сопротивление
которой равно R = 20 Ом. По истечении времени t = 0,1 с
сила тока замыкания достигла 95% от
предельного значения. Определить индуктивность катушки.
Дано:
R=20 Ом
t=0,1 с
k=95%=0,95
Определить:
L ‑ ?
Решение
Поскольку в
электрической цепи присутствует катушка, тогда, за счет возникновения э.д.с.
индукции в катушке, при замыкании контура в цепи ток будет со временем
нарастать до своего максимального значения по зависимости:
где I ‑ сила тока в
цепи на момент времени
 ; I0 ‑ максимальное
значение силы тока в цепи;  ‑ время
релаксации (то есть время, за которое сила тока в цепи изменяется в e раз)
Согласно
обозначению времени релаксации:
где L ‑ индуктивность катушки; I‑ активное сопротивление
цепи (в данном случае – катушки).
Согласно условию задачи:
Прологарифмируем полученное
уравнение:
     
Ответ: 0,67 Гн
В колебательном контуре с периодом колебаний
T = 100 мкс напряжение на
конденсаторе через промежуток времени t =
25 мкс, прошедший с момента, когда напряжение было равно нулю, составляет U= 500 В. Найти емкость конденсатора при общей энергии
контура, равной W = 1
мДж.
Дано:
T=100 мкс=10-4 с
t=25 мкс=25·10-6 с
U0=0 В
U=500 В
W=1 мДж=10-3 Дж
Определить:
C ‑ ?
Решение
Считая, что
активное сопротивление электрической цепи равно нулю, можно утверждать, что в
контуре происходят гармонические электромагнитные колебания, а значение заряда
на пластинках конденсатора изменяется по закону косинуса:
Согласно
определению силы тока:
 
Энергия
магнитного поля катушки:
Ответ: 8 нФ
Вагон массой 11 т
движется со скоростью 18 км/ч. Какова должна быть сила торможения, чтобы
остановить вагон на расстоянии 250 м?
 От двухступенчатой ракеты массой 1 т при скорости 1710 м/с отделилась её вторая ступень массой 0,4 т. Скорость второй ступени при этом увеличилась до 1860 м/с. Определить, с какой скоростью стала двигаться первая ступень ракеты.
По небольшому куску металла, лежащему на
наковальне, масса которой 300 кг, ударяет молот массой 8 кг. Определить КПД
удара, считая удар неупругим. Полезной энергией считать энергию, затраченную на
деформацию металла.
К
источнику тока параллельно подключены конденсатор емкостью 20мкФ и катушка
индуктивностью 0.02 Гн. Напряжение на конденсаторе 100В, ток в катушке 2А.
Затем источник отключают. Какой заряд будет на конденсаторе, когда ток в
катушке равен 1А?
 | |||
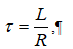
Немає коментарів:
Дописати коментар